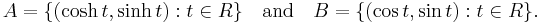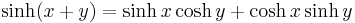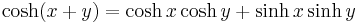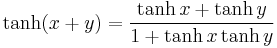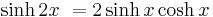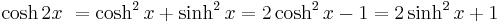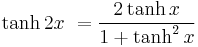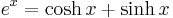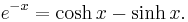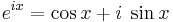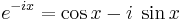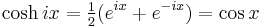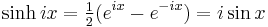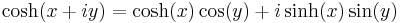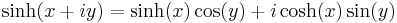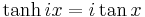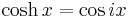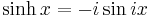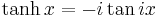Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" ( /ˈsɪntʃ/ or /ˈʃaɪn/), and the hyperbolic cosine "cosh" ( /ˈkɒʃ/), from which are derived the hyperbolic tangent "tanh" ( /ˈtæntʃ/ [1], and so on, corresponding to the derived trigonometric functions. The inverse hyperbolic functions are the area hyperbolic sine "arsinh" (also called "asinh" or sometimes "arcsinh")[2] and so on.
Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the right half of the equilateral hyperbola. Hyperbolic functions occur in the solutions of some important linear differential equations, for example the equation defining a catenary, and Laplace's equation in Cartesian coordinates. The latter is important in many areas of physics, including electromagnetic theory, heat transfer, fluid dynamics, and special relativity.
The hyperbolic functions take real values for a real argument called a hyperbolic angle. In complex analysis, they are simply rational functions of exponentials, and so are meromorphic.
Hyperbolic functions were introduced in the 1760s independently by Vincenzo Riccati and Johann Heinrich Lambert.[3] Riccati used Sc. and Cc. ([co]sinus circulare) to refer to circular functions and Sh. and Ch. ([co]sinus hyperbolico) to refer to hyperbolic functions. Lambert adopted the names but altered the abbreviations to what they are today.[4] The abbreviations sh and ch are still used in some other languages, like French and Russian.
Standard algebraic expressions
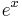 and
and 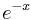
The hyperbolic functions are:
- Hyperbolic sine:
- Hyperbolic cosine:
- Hyperbolic tangent:
- Hyperbolic cotangent:
- Hyperbolic secant:
- Hyperbolic cosecant:
Hyperbolic functions can be introduced via imaginary circular angles:
- Hyperbolic sine:
- Hyperbolic cosine:
- Hyperbolic tangent:
- Hyperbolic cotangent:
- Hyperbolic secant:
- Hyperbolic cosecant:
where i is the imaginary unit defined as i2 = −1.
The complex forms in the definitions above derive from Euler's formula.
Note that, by convention, sinh2 x means (sinh x)2, not sinh(sinh x); similarly for the other hyperbolic functions when used with positive exponents. Another notation for the hyperbolic cotangent function is ctnh x, though coth x is far more common.
Useful relations
Hence:
It can be seen that cosh x and sech x are even functions; the others are odd functions.
Hyperbolic sine and cosine satisfy the identity
which is similar to the Pythagorean trigonometric identity. One also has
for the other functions.
The hyperbolic tangent is the solution to the nonlinear boundary value problem[5]:
It can be shown that the area under the curve of cosh x is always equal to the arc length:[6]
Inverse functions as logarithms
Derivatives
Standard Integrals
For a full list of integrals of hyperbolic functions, see list of integrals of hyperbolic functions
Where C is the constant of integration.
Taylor series expressions
It is possible to express the above functions as Taylor series:
The function sinh x has a Taylor series expression with only odd exponents for x. Thus it is an odd function, that is, −sinh x = sinh(−x), and sinh 0 = 0.
The function cosh x has a Taylor series expression with only even exponents for x. Thus it is an even function, that is, symmetric with respect to the y-axis. The sum of the sinh and cosh series is the infinite series expression of the exponential function.
where
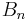 is the nth Bernoulli number
is the nth Bernoulli number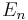 is the nth Euler number
is the nth Euler number
Comparison with circular trigonometric functions
Consider these two subsets of the Cartesian plane
Then A forms the right branch of the unit hyperbola {(x,y): x2 − y2 = 1}, while B is the unit circle. Evidently  = {(1,0)}. The primary difference is that the map t → B is a periodic function while t → A is not.
= {(1,0)}. The primary difference is that the map t → B is a periodic function while t → A is not.
There is a close analogy of A with B through split-complex numbers in comparison with ordinary complex numbers, and its circle group. In particular, the maps t → A and t → B are the exponential map in each case. They are both instances of one-parameter groups in Lie theory where all groups evolve out of the identity 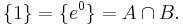 For contrast, in the terminology of topological groups, B forms a compact group while A is non-compact since it is unbounded.
For contrast, in the terminology of topological groups, B forms a compact group while A is non-compact since it is unbounded.
The hyperbolic functions satisfy many identities, all of them similar in form to the trigonometric identities. In fact, Osborn's rule[7] states that one can convert any trigonometric identity into a hyperbolic identity by expanding it completely in terms of integral powers of sines and cosines, changing sine to sinh and cosine to cosh, and switching the sign of every term which contains a product of 2, 6, 10, 14, ... sinhs. This yields for example the addition theorems
the "double argument formulas"
and the "half-argument formulas"[8]
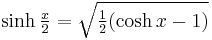 Note: This is equivalent to its circular counterpart multiplied by −1.
Note: This is equivalent to its circular counterpart multiplied by −1.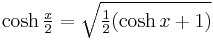 Note: This corresponds to its circular counterpart.
Note: This corresponds to its circular counterpart.
The derivative of sinh x is cosh x and the derivative of cosh x is sinh x; this is similar to trigonometric functions, albeit the sign is different (i.e., the derivative of cos x is −sin x).
The Gudermannian function gives a direct relationship between the circular functions and the hyperbolic ones that does not involve complex numbers.
The graph of the function a cosh(x/a) is the catenary, the curve formed by a uniform flexible chain hanging freely between two fixed points under uniform gravity.
Relationship to the exponential function
From the definitions of the hyperbolic sine and cosine, we can derive the following identities:
and
These expressions are analogous to the expressions for sine and cosine, based on Euler's formula, as sums of complex exponentials.
Hyperbolic functions for complex numbers
Since the exponential function can be defined for any complex argument, we can extend the definitions of the hyperbolic functions also to complex arguments. The functions sinh z and cosh z are then holomorphic.
Relationships to ordinary trigonometric functions are given by Euler's formula for complex numbers:
so:
Thus, hyperbolic functions are periodic with respect to the imaginary component,with period 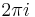 (
(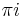 for hyperbolic tangent and cotangent).
for hyperbolic tangent and cotangent).
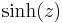 |
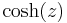 |
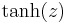 |
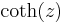 |
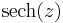 |
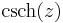 |
See also
- Catenary
- e (mathematical constant)
- Equal incircles theorem, based on sinh
- List of integrals of hyperbolic functions
- Poinsot's spirals
- Sigmoid function
References
- ^ tanh
- ^ Some examples of using arcsinh found in Google Books.
- ^ Robert E. Bradley, Lawrence A. D'Antonio, Charles Edward Sandifer. Euler at 300: an appreciation. Mathematical Association of America, 2007. Page 100.
- ^ Georg F. Becker. Hyperbolic functions. Read Books, 1931. Page xlviii.
- ^ Eric W. Weisstein. "Hyperbolic Tangent". MathWorld. http://mathworld.wolfram.com/HyperbolicTangent.html. Retrieved 2008-10-20.
- ^ N.P., Bali (2005). Golden Intergral Calculus. Firewall Media. p. 472. ISBN 8-170-08169-6. http://books.google.com/books?id=hfi2bn2Ly4cC., Extract of page 472
- ^ G. Osborn, Mnemonic for hyperbolic formulae, The Mathematical Gazette, p. 189, volume 2, issue 34, July 1902
- ^ Peterson, John Charles (2003). Technical mathematics with calculus (3rd ed.). Cengage Learning. p. 1155. ISBN 0-766-86189-9. http://books.google.com/books?id=PGuSDjHvircC., Chapter 26, page 1155
External links
- Hyperbolic functions on PlanetMath
- Hyperbolic functions entry at MathWorld
- GonioLab: Visualization of the unit circle, trigonometric and hyperbolic functions (Java Web Start)
- Web-based calculator of hyperbolic functions
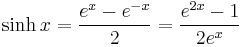
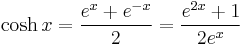
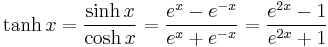
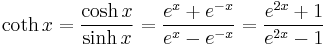
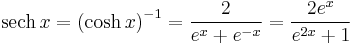
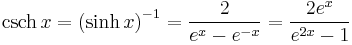
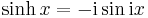
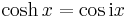
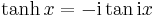
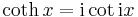
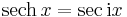
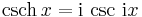

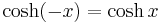
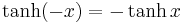

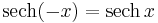
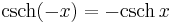
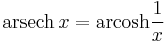
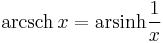
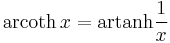
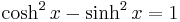
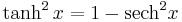
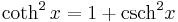
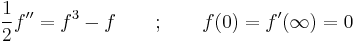
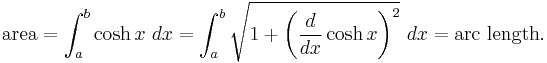
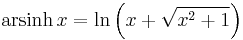
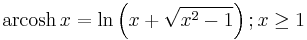
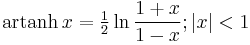
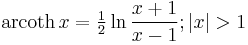
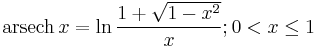
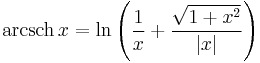
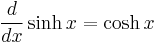
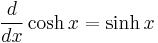
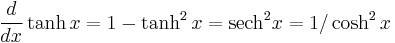
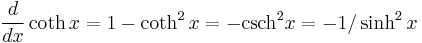
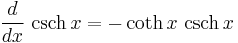
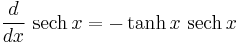
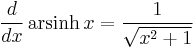
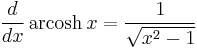
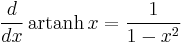
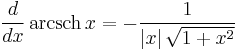
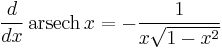
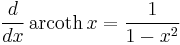
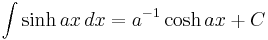
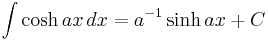
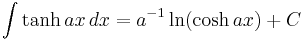
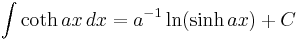
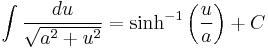
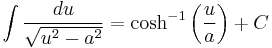
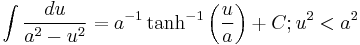
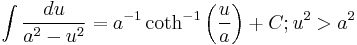
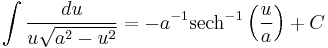
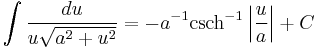
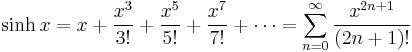
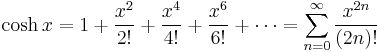
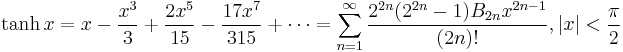
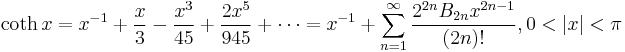 (
(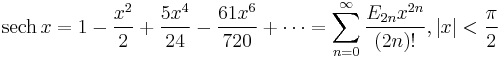
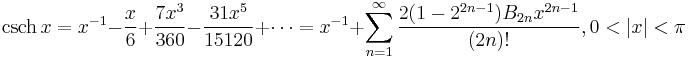 (
(